888 Appendix A: Functions and Instructions
tanhê() MATH/Hyperbolic menu
tanhê(
expression1
) ⇒
⇒⇒
⇒
expression
tanhê(
list1
) ⇒
⇒⇒
⇒
list
tanhê(
expression1
) returns the inverse hyperbolic
tangent of the argument as an expression.
tanhê(
list1
) returns a list of the inverse
hyperbolic tangents of each element of
list1
.
In rectangular complex format mode:
tanhê (0) ¸ 0
tanh
ê ({1,2.1,3}) ¸
{
ˆ .518... ì1.570...ø
i
ln(2)
2
ì
p
2
ø
i
}
tanhê(
squareMatrix1
) ⇒
⇒⇒
⇒
squareMatrix
Returns the matrix inverse hyperbolic tangent of
squareMatrix1
. This is
not
the same as calculating
the inverse hyperbolic tangent of each element.
For information about the calculation method,
refer to
cos().
squareMatrix1
must be diagonalizable. The result
always contains floating-point numbers.
In Radian angle mode and Rectangular complex
format mode:
tanhê([1,5,3;4,2,1;6,ë2,1]) ¸
ë.099…+.164…ø
i
.267…ì 1.490…ø
i
…
ë.087…ì.725…ø
i
.479…ì.947…ø
i
…
.511…ì 2.083…ø
i
ë.878…+1.790…ø
i
…
taylor() MATH/Calculus menu
taylor(
expression1
,
var
,
order
[,
point
]) ⇒
⇒⇒
⇒
expression
Returns the requested Taylor polynomial. The
polynomial includes non-zero terms of integer
degrees from zero through
order
in (
var
minus
point
). taylor() returns itself if there is no
truncated power series of this order, or if it would
require negative or fractional exponents. Use
substitution and/or temporary multiplication by a
power of
(
var
minus
point
) to determine more general
power series.
point
defaults to zero and is the expansion point.
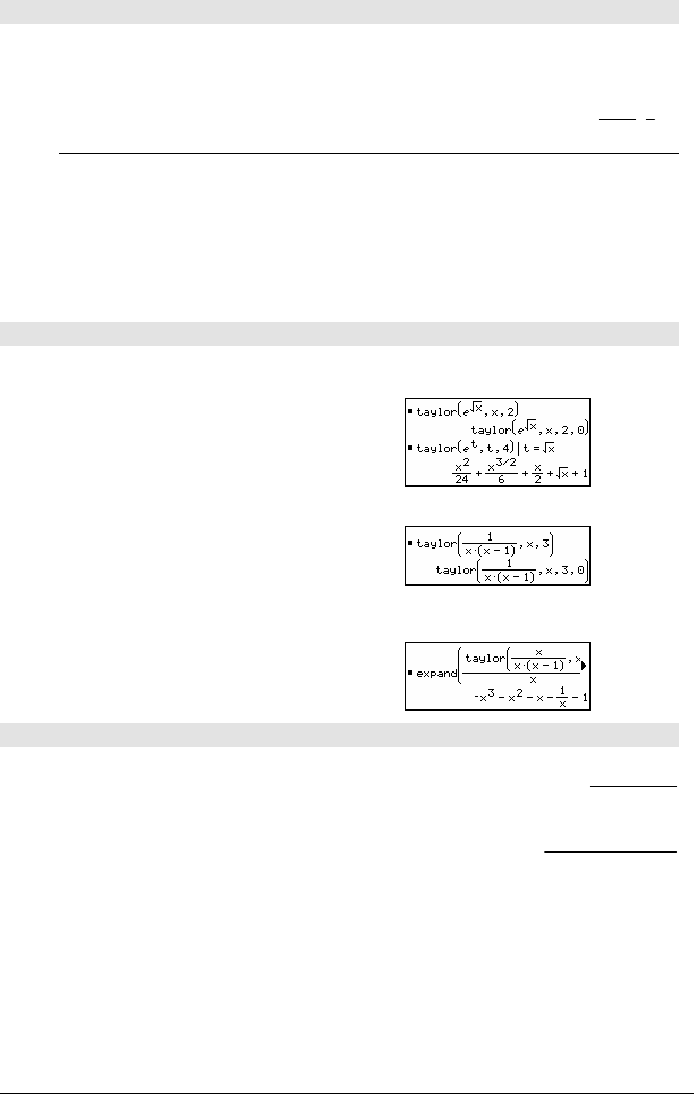
taylor(
e
^(‡(x)),x,2) ¸
taylor(
e
^(t),t,4)|t=‡(x) ¸
taylor(1/(x
ù (xì1)),x,3) ¸
expand(taylor(x/(x
ù(xì1)),
x,4)/x,x)
¸
tCollect() MATH\Algebra\Trig menu
tCollect(
expression1
) ⇒
⇒⇒
⇒
expression
Returns an expression in which products and
integer powers of sines and cosines are converted
to a linear combination of sines and cosines of
multiple angles, angle sums, and angle
differences. The transformation converts
trigonometric polynomials into a linear
combination of their harmonics.
Sometimes
tCollect() will accomplish your goals
when the default trigonometric simplification
does not.
tCollect() tends to reverse
transformations done by
tExpand(). Sometimes
applying
tExpand() to a result from tCollect(),
or vice versa, in two separate steps simplifies an
expression.
tCollect((cos(a))^2) ¸
cos(2
ø a) + 1
2
tCollect(sin(
a)cos(b)) ¸
sin(
aì b)+sin(a+b)
2


















