104
Example 6
The Wheaton data depart significantly from Model A.
Dealing with Rejection
You have several options when a proposed model has to be rejected on statistical
grounds:
You can point out that statistical hypothesis testing can be a poor tool for choosing
a model. Jöreskog (1967) discussed this issue in the context of factor analysis. It is
a widely accepted view that a model can be only an approximation at best, and that,
fortunately, a model can be useful without being true. In this view, any model is
bound to be rejected on statistical grounds if it is tested with a big enough sample.
From this point of view, rejection of a model on purely statistical grounds
(particularly with a large sample) is not necessarily a condemnation.
You can start from scratch to devise another model to substitute for the rejected one.
You can try to modify the rejected model in small ways so that it fits the data better.
It is the last tactic that will be demonstrated in this example. The most natural way of
modifying a model to make it fit better is to relax some of its assumptions. For
example, Model A assumes that eps1 and eps3 are uncorrelated. You could relax this
restriction by connecting eps1 and eps3 with a double-headed arrow. The model also
specifies that anomia67 does not depend directly on ses. You could remove this
assumption by drawing a single-headed arrow from ses to anomia67. Model A does
not happen to constrain any parameters to be equal to other parameters, but if such
constraints were present, you might consider removing them in hopes of getting a
better fit. Of course, you have to be careful when relaxing the assumptions of a model
that you do not turn an identified model into an unidentified one.
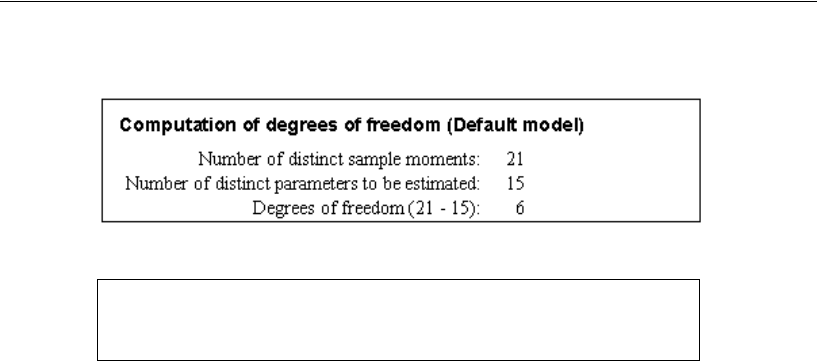
Chi-square = 71.544
Degrees of freedom = 6
Probability level = 0.000


















