476
Example 32
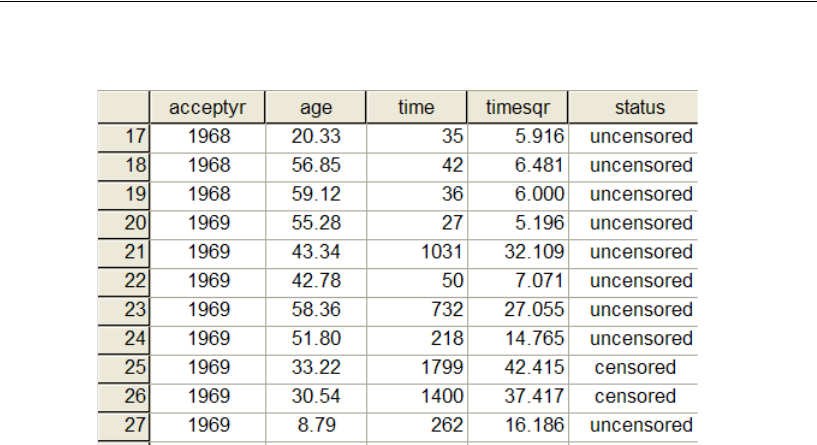
Reading across the first visible row in the figure above, Patient 17 was accepted into
the program in 1968. The patient at that time was 20.33 years old. The patient died 35
days later. The next number, 5.916, is the square root of 35. Amos assumes that
censored variables are normally distributed. The square root of survival time will be
used in this example in the belief that it is probably more nearly normally distributed
than is survival time itself.
Uncensored simply means that we know how long the
patient lived. In other words, the patient has already died, and that is how we are able
to tell that he lived for 35 days after being admitted into the program.
Some patients were still alive when last seen. For example, Patient 25 entered the
program in 1969 at the age of 33.22 years. The patient was last seen 1,799 days later.
The number 42.415 is the square root of 1,799. The word
censored in the Status column
means that the patient was still alive 1,799 days after being accepted into the program,
and that is the last time the patient was seen. So, we can’t say that the patient survived
for 1,799 days. In fact, he survived for longer than that; we just don’t know how much
longer. There are more cases like that. Patient number 26 was last seen 1,400 days after
acceptance into the program and, at that time, was still alive, so we know that that
patient lived for at least 1,400 days.
It is not clear what is to be done with a censored value like Patient 25’s survival time
of 1,799 days. You can’t just discard the 1,799 and all the other censored values
because that amounts to discarding the patients who lived a long time. On the other
hand, you can’t keep the 1,799 and treat it as an ordinary score because you know the
patient really lived for more than 1,799 days.
In Amos, you can use the information that Patient 25 lived for more than 1,799 days,
neither discarding the information nor pretending that the patient’s survival time is


















