232
Example 15
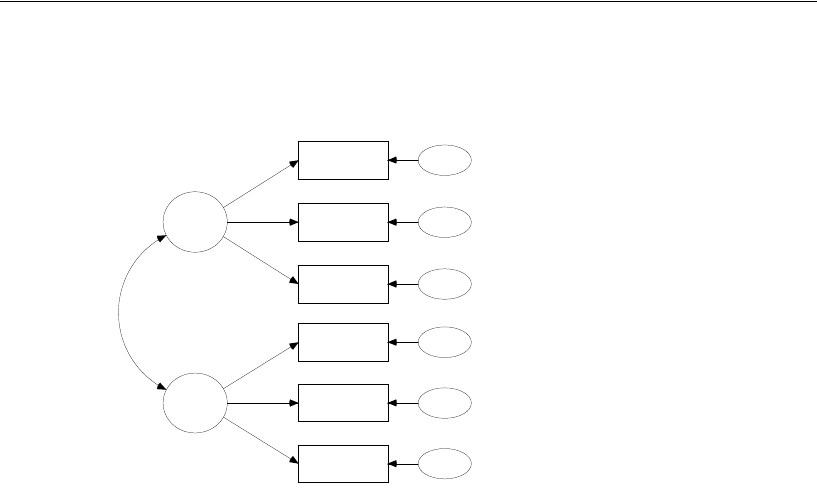
The boys’ path diagram should look like this:
Understanding the Cross-Group Constraints
The cross-group constraints on intercepts and regression weights may or may not be
satisfied in the populations. One result of fitting the model will be a test of whether
these constraints hold in the populations of girls and boys. The reason for starting out
with these constraints is that (as Sörbom points out) it is necessary to impose some
constraints on the intercepts and regression weights in order to make the model
identified when estimating factor means. These are not the only constraints that would
make the model identified, but they are plausible ones.
The only difference between the boys’ and girls’ path diagrams is in the constraints
on the two factor means. For boys, the means are fixed at 0. For girls, both factor means
are estimated. The girls’ factor means are named mn_s and mn_v, but the factor means
are unconstrained because each mean has a unique name.
The boys’ factor means were fixed at 0 in order to make the model identified.
Sörbom showed that, even with all the other constraints imposed here, it is still not
possible to estimate factor means for both boys and girls simultaneously. Take verbal
ability, for example. If you fix the boys’ mean verbal ability at some constant (like 0),
you can then estimate the girls’ mean verbal ability. Alternatively, you can fix the girls’
mean verbal ability at some constant, and then estimate the boys’ mean verbal ability.
The bad news is that you cannot estimate both means at once. The good news is that
0,
spatial
int_vis
visperc
int_cub
cubes
int_loz
lozenges
int_wrd
wordmean
int_par
paragrap
int_sen
sentence
0,
err_v
0,
err_c
0,
err_l
0,
err_p
0,
err_s
0,
err_w
0,
verbal
1
cube_s
lozn_s
1
sent_v
word_v
1
1
1
1
1
1


















