394
Example 26
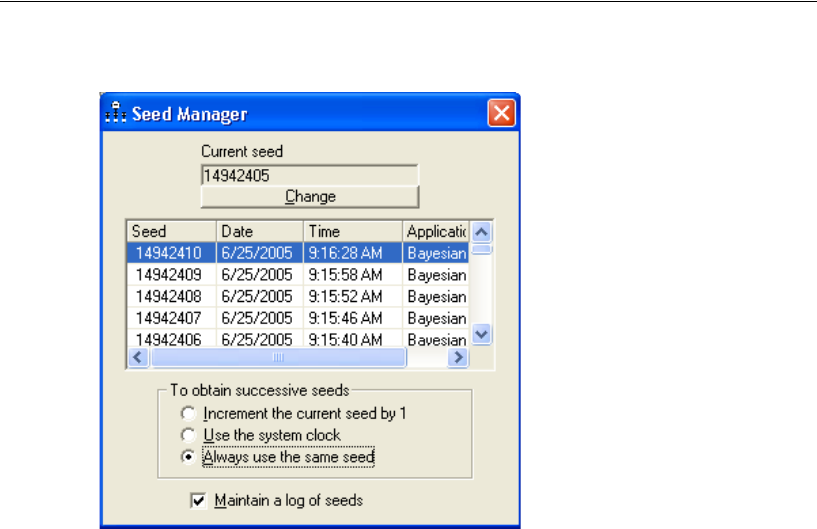
Record the value of this seed in a safe place so that you can replicate the results of your
analysis at a later date.
Tip: We use the same seed value of 14942405 for all examples in this guide so that you
can reproduce our results.
We mentioned earlier that the MCMC algorithm used by Amos draws random values
of parameters from high-dimensional joint posterior distributions via Monte Carlo
simulation of the posterior distribution of parameters. For instance, the value reported
in the Mean column is not the exact posterior mean but is an estimate obtained by
averaging across the random samples produced by the MCMC procedure. It is
important to have at least a rough idea of how much uncertainty in the posterior mean
is attributable to Monte Carlo sampling.
The second column, labeled S.E., reports an estimated standard error that suggests
how far the Monte-Carlo estimated posterior mean may lie from the true posterior
mean. As the MCMC procedure continues to generate more samples, the estimate of
the posterior mean becomes more precise, and the S.E. gradually drops. Note that this
S.E. is not an estimate of how far the posterior mean may lie from the unknown true
value of the parameter. That is, one would not use ± 2 S.E. values as the width of a
95% interval for the parameter.
