76 Chapter 3: Symbolic Manipulation
03SYMBOL.DOC TI-89/TI-92 Plus: Symbolic Manipulation (English) Susan Gullord Revised: 02/23/01 10:52 AM Printed: 02/23/01 2:12 PM Page 76 of 24
Use the
‰
integrate
(
…
2
) and d
differentiate
(
…
1
) functions.
‰
(expression, var [,low] [,up])
d
(expression, var [,order])
Integrate
x
ñù
sin(x)
with respect
to
x
.
Differentiate the answer with
respect to
x
.
Use the
limit
(
…
3
) function.
limit
(expression, var, point [,direction])*
Find the limit of
sin(3x) / x
as
x
approaches
0
.
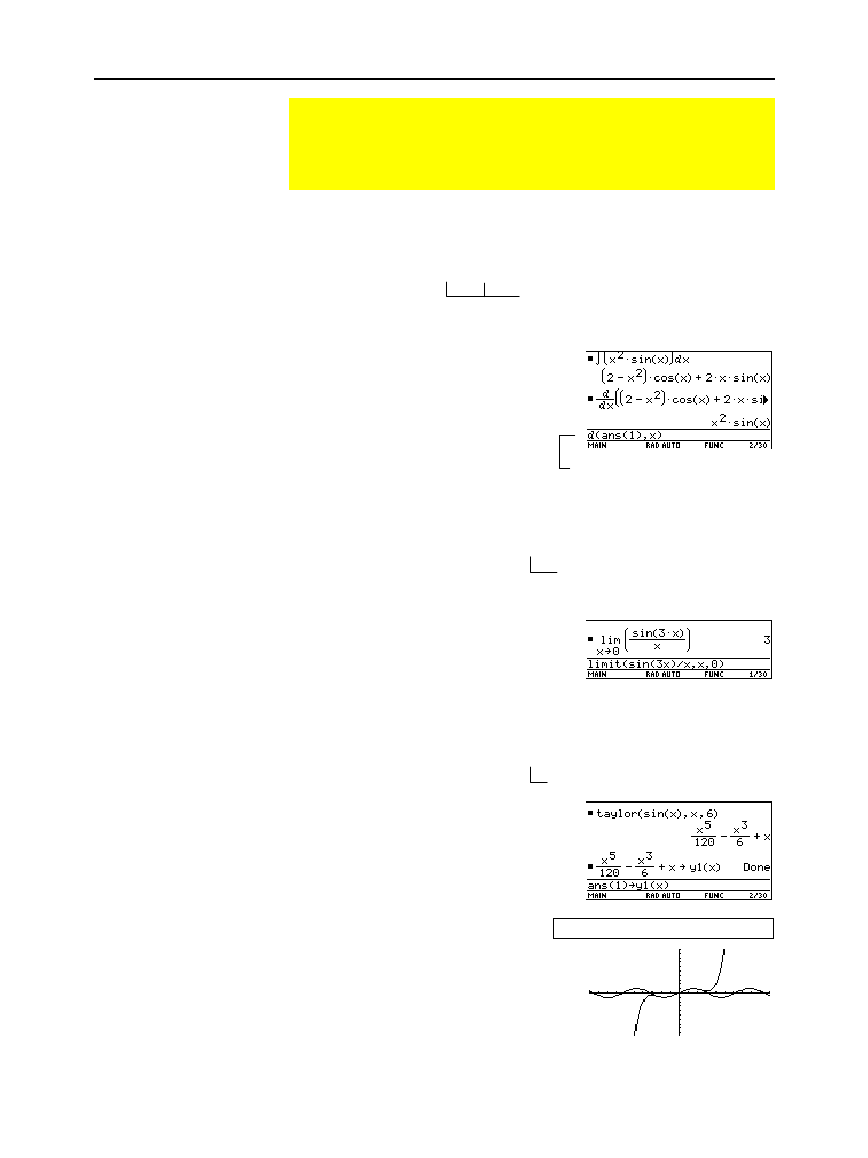
Use the
taylor
(
…
9
) function.
taylor
(expression, var, order [,point])
Find a 6th order Taylor
polynomial for
sin(x)
with
respect to
x
.
Store the answer as a user-
defined function named
y1(x)
.
Then graph
sin(x)
and the Taylor
polynomial.
Graph sin(x):Graph y1(x)
Common Calculus Operations
This section gives examples for some of the functions
available from the
…
Calc
toolbar menu. For complete
information about any calculus function, refer to Appendix A.
Integrating and
Differentiating
Note:
You can integrate an
expression only; you can
differentiate an expression,
list, or matrix.
Finding a Limit
Note:
You can find a limit
for an expression, list, or
matrix.
Finding a Taylor
Polynomial
Important:
Degree-mode
scaling by
p
/180 may cause
calculus application results
to appear in a different form.
lets you specify limits or a
constant of integration
To get d, use
…
1 or
2
=
.
Do not simply type the letter D
on the keyboard.
negative = from left
positive = from right
omitted or 0 = both
if omitted, expansion point is 0


















