Page 7-6
discharge (m
3
/s or ft
3
/s), A is the cross-sectional area (m
2
or ft
2
), C
u
is a
coefficient that depends on the system of units (C
u
= 1.0 for the SI, C
u
= 1.486
for the English system of units), n is the Manning’s coefficient, a measure of the
channel surface roughness (e.g., for concrete, n = 0.012), P is the wetted
perimeter of the cross section (m or ft), S
o
is the slope of the channel bed
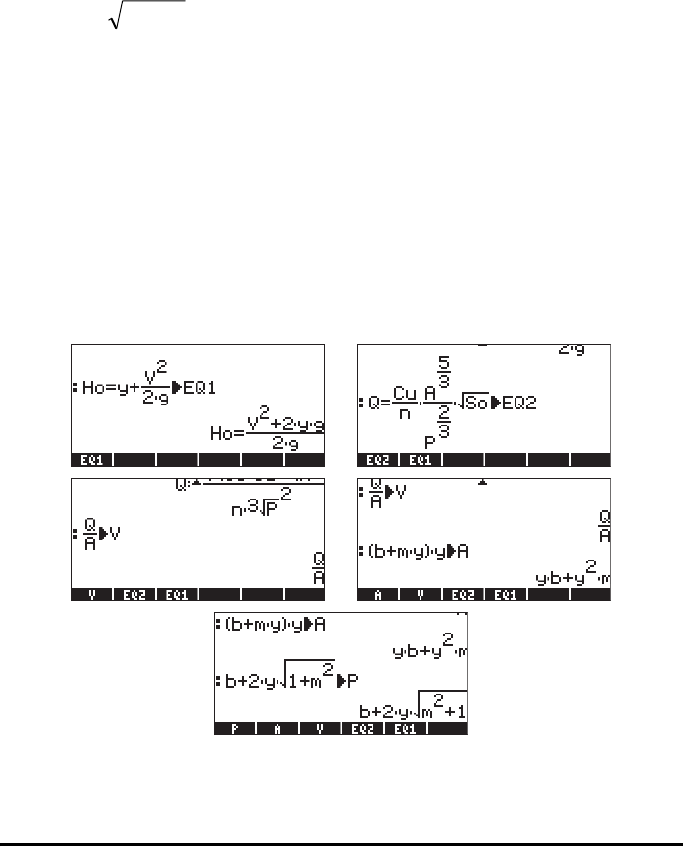
expressed as a decimal fraction. For a trapezoidal channel, as shown below,
the area is given by , while the wetted perimeter is given by
, where b is the bottom width (m or ft), and m is the side
slope (1V:mH) of the cross section.
Typically, one has to solve the equations of energy and Manning’s
simultaneously for y and Q. Once these equations are written in terms of the
primitive variables b, m, y, g, S
o
, n, Cu, Q, and H
o
, we are left with a system of
equations of the form f
1
(y,Q) = 0, f
2
(y,Q) = 0. We can build these two
equations as follows.
We assume that we will be using the ALG and Exact modes in the calculator,
although defining the equations and solving them with MSLV is very similar in
the RPN mode. Create a sub-directory, say CHANL (for open CHANneL), and
within that sub-directory define the following variables:
To see the original equations, EQ1 and EQ2, in terms of the primitive variables
listed above, we can use function EVAL applied to each of the equations, i.e.,
ymybA )( +=
2
12 mybP ++=


















