Filter
Top Products
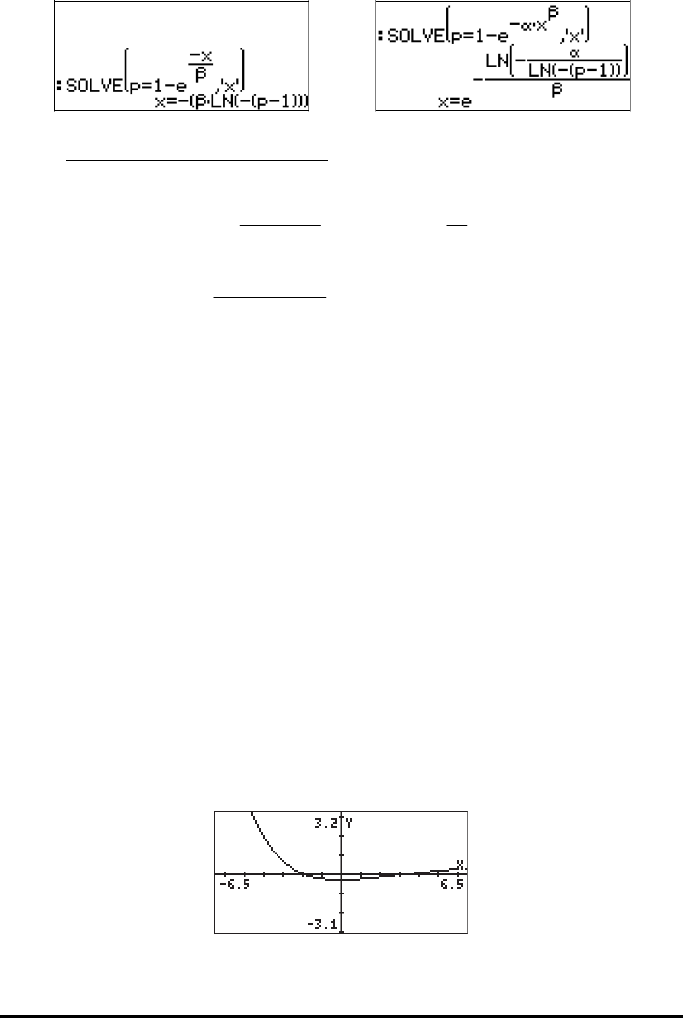
Page 17-14
Exponential: Weibull:
For the Gamma and Beta distributions
the expressions to solve will be more
complicated due to the presence of integrals, i.e.,
• Gamma,
• Beta,
A numerical solution with the numerical solver will not be feasible because of
the integral sign involved in the expression. However, a graphical solution is
possible. Details on how to find the root of a graph are presented in Chapter
12. To ensure numerical results, change the CAS setting to Approx. The
function to plot for the Gamma distribution is
Y(X) = ∫(0,X,z^(
α-1)*exp(-z/β)/(β^α*GAMMA(α)),z)-p
For the Beta distribution, the function to plot is
Y(X) =
∫(0,X,z^(
α-1)*(1-z)^(β-1)*GAMMA(α+β)/(GAMMA(α)*GAMMA(β)),z)-p
To produce the plot, it is necessary to store values of
α, β, and p, before
attempting the plot. For example, for
α = 2, β = 3, and p = 0.3, the plot of
Y(X) for the Gamma distribution is shown below. (Please notice that, because of
the complicated nature of function Y(X), it will take some time before the graph
is produced. Be patient.)
∫
−⋅⋅
Γ
=
−
x
dz
z
zp
0
1
)exp(
)(
1
β
αβ
α
α
∫
−−
−⋅⋅
Γ⋅Γ
+Γ
=
x
dzzzp
0
11
)1(
)()(
)(
βα
βα
βα