Page 11-6
In algebraic mode, the keystrokes are: [enter or select the matrix] Q [enter the
power] `. In RPN mode, the keystrokes are: [enter or select the matrix] †
[enter the power] Q`.
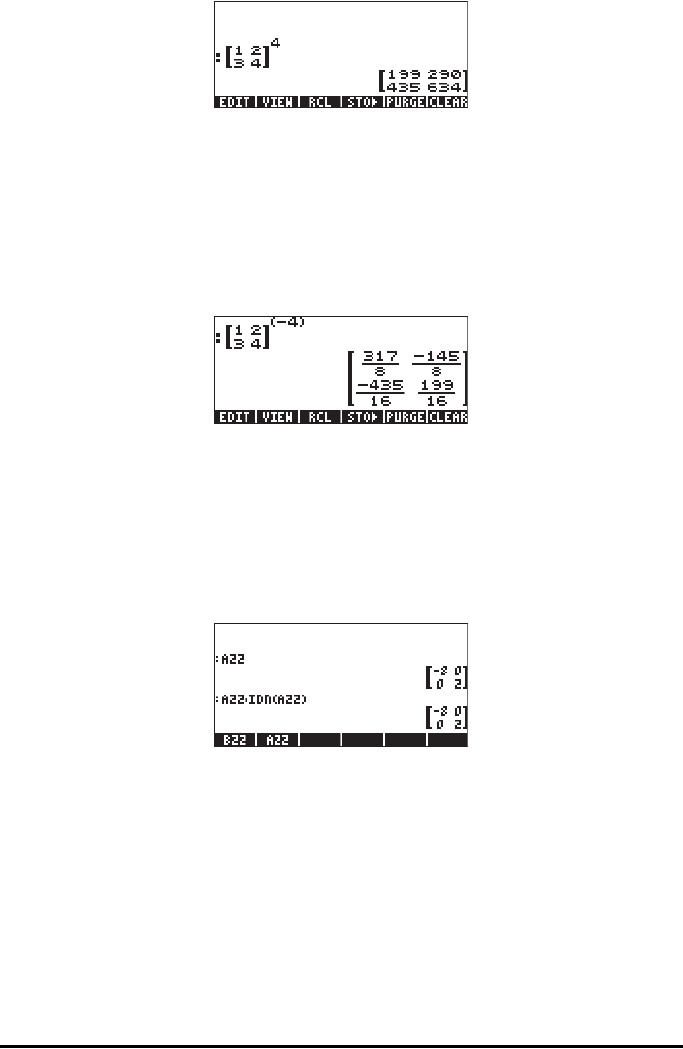
Matrices can be raised to negative powers. In this case, the result is equivalent
to 1/[matrix]^ABS(power).
The identity matrix
In Chapter 9 we introduce the identity matrix as the matrix I = [δ
ij
]
n×n
, where δ
ij
is the Kronecker’s delta function. Identity matrices can be obtained by using
function IDN described in Chapter 9. The identity matrix has the property that
A⋅I = I⋅A = A. To verify this property we present the following examples using
the matrices stored earlier on:
The inverse matrix
The inverse of a square matrix A is the matrix A
-1
such that A⋅A
-1
= A
-1
⋅A = I,
where I is the identity matrix of the same dimensions as A. The inverse of a
matrix is obtained in the calculator by using the inverse function, INV (i.e., the
Y key). An example of the inverse of one of the matrices stored earlier is
presented next:





















