Filter
Top Products
Page 11-3
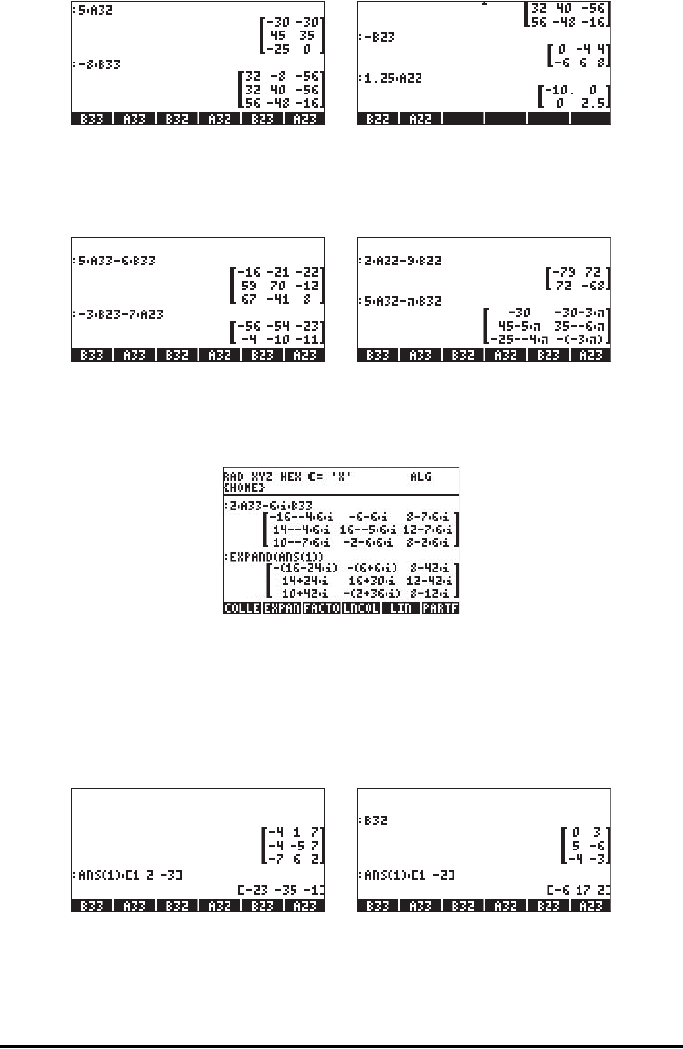
By combining addition and subtraction with multiplication by a scalar we can
form linear combinations of matrices of the same dimensions, e.g.,
In a linear combination of matrices, we can multiply a matrix by an imaginary
number to obtain a matrix of complex numbers, e.g.,
Matrix-vector multiplication
Matrix-vector multiplication is possible only if the number of columns of the
matrix is equal to the length of the vector. This operation follows the rules of
matrix multiplication as shown in the next section. A couple of examples of
matrix-vector multiplication follow:
Vector-matrix multiplication, on the other hand, is not defined. This
multiplication can be performed, however, as a special case of matrix
multiplication as defined next.