Page 11-1
Chapter 11
Matrix Operations and Linear Algebra
In Chapter 10 we introduced the concept of a matrix and presented a number
of functions for entering, creating, or manipulating matrices. In this Chapter we
present examples of matrix operations and applications to problems of linear
algebra.
Operations with matrices
Matrices, like other mathematical objects, can be added and subtracted. They
can be multiplied by a scalar, or among themselves. They can also be raised to
a real power. An important operation for linear algebra applications is the
inverse of a matrix. Details of these operations are presented next.
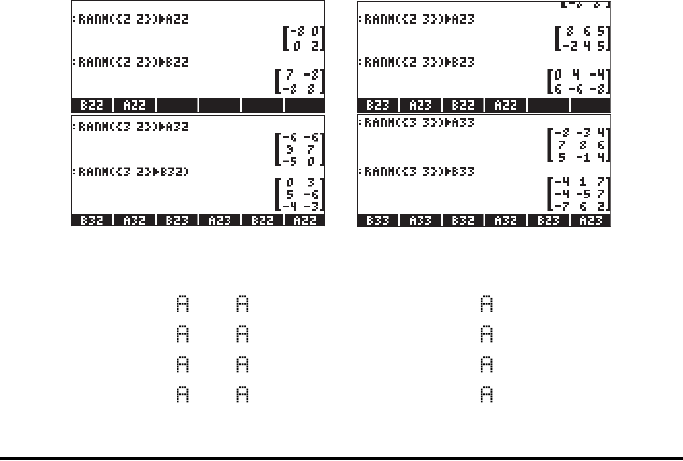
To illustrate the operations we will create a number of matrices that we will store
in variables. The generic name of the matrices will be Aij and Bij, where i
represents the number of rows and j the number of columns of the matrices. The
matrices to be used are generated by using function RANM (random matrices).
If you try this exercise in your calculator you will get different matrices than the
ones listed herein, unless you store them into your calculator exactly as shown
below. Here are the matrices A22, B22, A23, B23, A32, B32, A33 and B33
created in ALG mode:
In RPN mode, the steps to follow are:
{2,2}` RNM'22'K {2,2}` R NM 'B22'K
{2,3}` RNM'23'K {2,3}` R NM 'B23'K
{3,2}` RNM'32'K {3,2}` R NM 'B32'K
{3,3}` RNM'33'K {3,3}` R NM 'B33'K


















