Filter
Top Products
Page 18-33
These results assume that the values s
1
and s
2
are the population standard
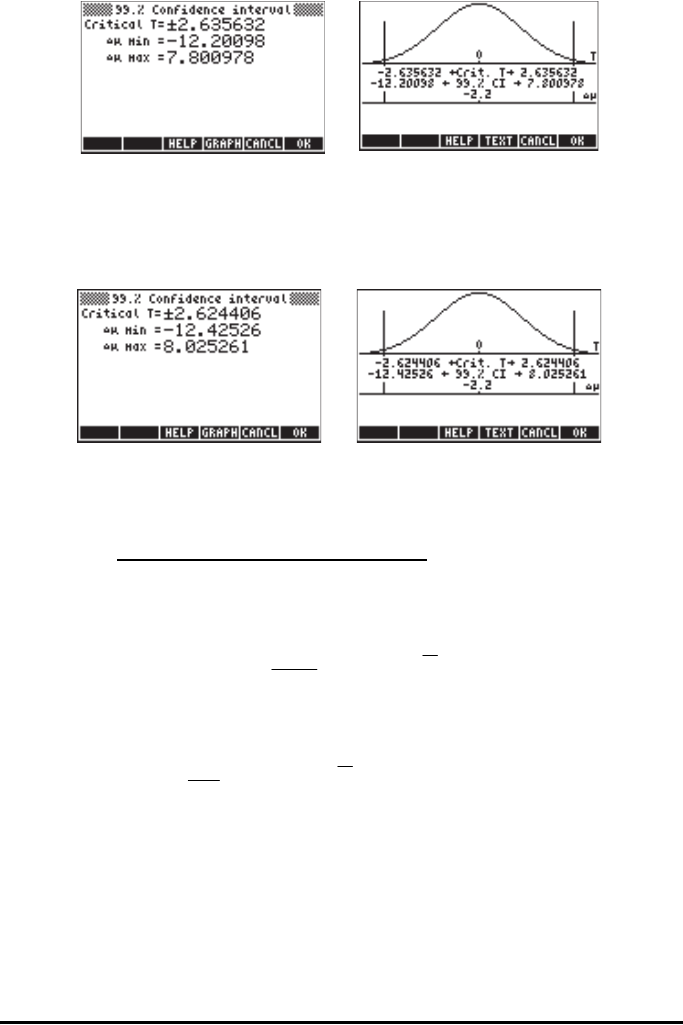
deviations. If these values actually represent the samples’ standard deviations,
you should enter the same values as before, but with the option
_pooled
selected. The results now become:
Confidence intervals for the variance
To develop a formula for the confidence interval for the variance, first we
introduce the sampling distribution of the variance
: Consider a random sample
X
1
, X
2
..., X
n
of independent normally-distributed variables with mean μ,
variance σ
2
, and sample mean ⎯X. The statistic
is an unbiased estimator of the variance σ
2
.
The quantity has a χ
n-1
2
(chi-square)
distribution with ν = n-1 degrees of freedom. The (1-α)⋅100 % two-sided
confidence interval is found from
Pr[χ
2
n-1,1-α/2
< (n-1)⋅S
2
/σ
2
< χ
2
n-1,α/2
] = 1- α.
∑
=
−⋅
−
=
n
i
i
XX
n
S
1
22
,)(
1
1
ˆ
∑
=
−=⋅−
n
i
i
XX
S
n
1
2
2
2
,)(
ˆ
)1(
σ