Page 16-24
where H(t) is Heaviside’s step function. Using Laplace transforms, we can
write: L{d
2
y/dt
2
+y} = L{H(t-3)}, L{d
2
y/dt
2
} + L{y(t)} = L{H(t-3)}. The last term in
this expression is: L{H(t-3)} = (1/s)⋅e
–3s
. With Y(s) = L{y(t)}, and L{d
2
y/dt
2
} =
s
2
⋅Y(s) - s⋅y
o
– y
1
, where y
o
= h(0) and y
1
= h’(0), the transformed equation is
s
2
⋅Y(s) – s⋅y
o
– y
1
+ Y(s) = (1/s)⋅e
–3s
. Change CAS mode to Exact, if
necessary. Use the calculator to solve for Y(s), by writing:
‘X^2*Y-X*y0-y1+Y=(1/X)*EXP(-3*X)’ ` ‘Y’ ISOL
The result is ‘Y=(X^2*y0+X*y1+EXP(-3*X))/(X^3+X)’.
To find the solution to the ODE, y(t), we need to use the inverse Laplace
transform, as follows:
OBJ ƒ ƒ Isolates right-hand side of last expression
ILAP Obtains the inverse Laplace transform
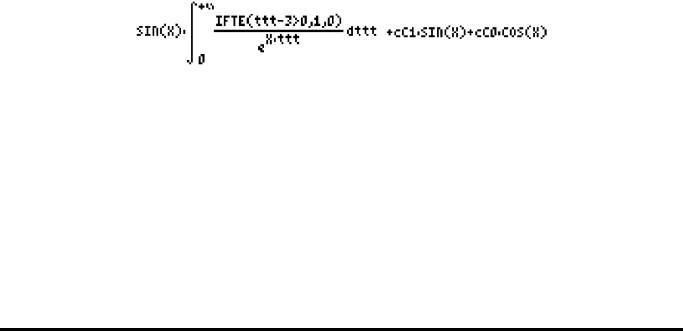
The result is ‘y1*SIN(X-1)+y0*COS(X-1)-(COS(X-3)-1)*Heaviside(X-3)’.
Thus, we write as the solution: y(t) = y
o
cos t + y
1
sin t + H(t-3)⋅(1+sin(t-3)).
Check what the solution to the ODE would be if you use the function LDEC:
‘H(X-3)’ `[ENTER] ‘X^2+1’ ` LDEC
The result is:
Please notice that the variable X in this expression actually represents the
variable t in the original ODE, and that the variable ttt in this expression is a
dummy variable. Thus, the translation of the solution in paper may be written
as:
.)3(sinsincos)(
0
1
∫
∞
−
⋅⋅−⋅+⋅+⋅= dueuHttCtCoty
ut


















