Filter
Top Products
Page 18-12
Where s
x
, s
y
are the standard deviations of x and y, respectively, i.e.
The values s
xy
and r
xy
are the "Covariance" and "Correlation," respectively,
obtained by using the "Fit data" feature of the calculator.
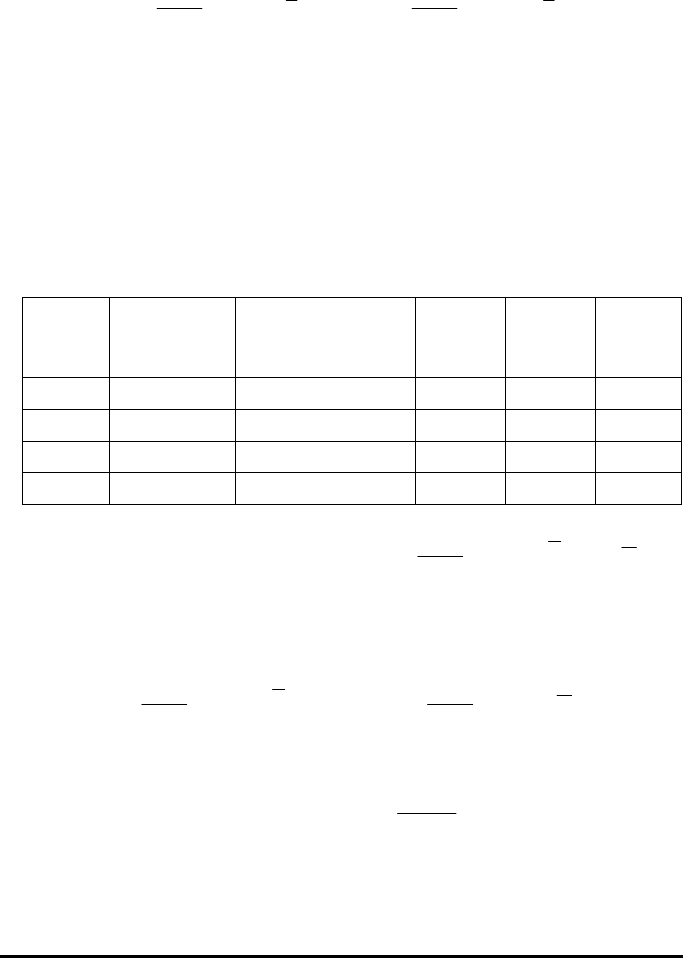
Linearized relationships
Many curvilinear relationships "straighten out" to a linear form. For example,
the different models for data fitting provided by the calculator can be linearized
as described in the table below.
The sample covariance of ξ,η is given by
Also, we define the sample variances of ξ and η, respectively, as
The sample correlation coefficient r
ξη
is
Indep. Depend.
Type of Actual Linearized variable Variable Covar.
Fitting Model Model
ξη
s
ξη
Linear y = a + bx [same] x y s
xy
Log. y = a + b ln(x) [same] ln(x) y s
ln(x),y
Exp.
y = a e
bx
ln(y) = ln(a) + bx x ln(y) s
x,ln(y)
Power
y = a x
b
ln(y) = ln(a) + b ln(x) ln(x) ln(y) s
ln(x),ln(y)
2
1
2
)(
1
1
xx
n
s
n
i
ix
−
−
=
∑
=
2
1
2
)(
1
1
yy
n
s
n
i
iy
−
−
=
∑
=
))((
1
1
ηηξξ
ξη
−−
−
=
∑
ii
n
s
2
1
2
)(
1
1
ξξ
ξ
−
−
=
∑
=
n
i
i
n
s
2
1
2
)(
1
1
ηη
η
−
−
=
∑
=
n
i
i
n
s
ηξ
ξη
ξη
ss
s
r
⋅
=