Page 19-1
Chapter 19
Numbers in Different Bases
In this Chapter we present examples of calculations of number in bases other
than the decimal basis.
Definitions
The number system used for everyday arithmetic is known as the decimal system
for it uses 10 (Latin, deca) digits, namely 0-9, to write out any real number.
Computers, on the other hand, use a system that is based on two possible
states, or binary system. These two states are represented by 0 and 1, ON
and OFF, or high-voltage and low-voltage. Computers also use number
systems based on eight digits (0-7) or octal system, and sixteen digits (0-9, A-F)
or hexadecimal. As in the decimal system, the relative position of digits
determines its value. In general, a number n in base b can be written as a
series of digits n = (a
1
a
2
…a
n
.c
1
c
2
…c
m
)
b
. The “point” separates n “integer”
digits from m “decimal” digits. The value of the number, converted to our
customary decimal system, is calculated by using n = a
1
⋅
bn
-1
+ a
2
⋅
b
n-2
+ … +
a
n
b
0
+ c
1
⋅
b
-1
+ c
2
⋅
b
-2
+ … +c
m
⋅
b
-m
. For example, (15.234)
10
= 1⋅10
1
+
5⋅10
0
+ 2⋅10
-1
+ 3⋅10
-2
+ 4⋅10
-3
, and (101.111)
2
= 1⋅2
2
+ 0⋅2
1
+ 1⋅2
0
+
1⋅2
-1
+ 1⋅2
-2
+ 1⋅2
-3
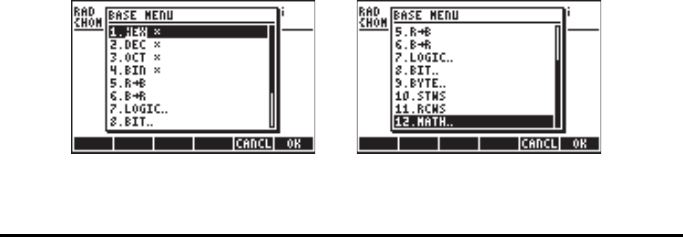
The BASE menu
While the calculator would typically be operated using the decimal system, you
can produce calculations using the binary, octal, or hexadecimal system.
Many of the functions for manipulating number systems other than the decimal
system are available in the BASE menu, accessible through ‚ã(the 3
key). With system flag 117 set to CHOOSE boxes, the BASE menu shows the
following entries:


















