Page 11-29
[[14,9,-2],[2,-5,2],[5,19,12]] `
[[1,2,3],[3,-2,1],[4,2,-1]] `/
The result of this operation is:
Gaussian and Gauss-Jordan elimination
Gaussian elimination is a procedure by which the square matrix of coefficients
belonging to a system of n linear equations in n unknowns is reduced to an
upper-triangular matrix (echelon form) through a series of row operations. This
procedure is known as forward elimination. The reduction of the coefficient
matrix to an upper-triangular form allows for the solution of all n unknowns,
utilizing only one equation at a time, in a procedure known as backward
substitution.
Example of Gaussian elimination using equations
To illustrate the Gaussian elimination procedure we will use the following system
of 3 equations in 3 unknowns:
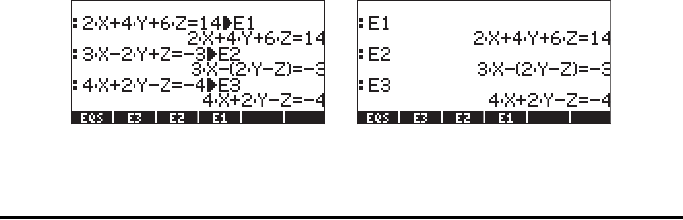
2X +4Y+6Z = 14,
3X -2Y+ Z = -3,
4X +2Y -Z = -4.
We can store these equations in the calculator in variables E1, E2, and E3,
respectively, as shown below. For backup purposes, a list containing the three
equations was also created and stored into variable EQS. This way, if a
mistake is made, the equations will still be available to the user.
.
213
152
221
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
=
X


















