Filter
Top Products
Page 18-30
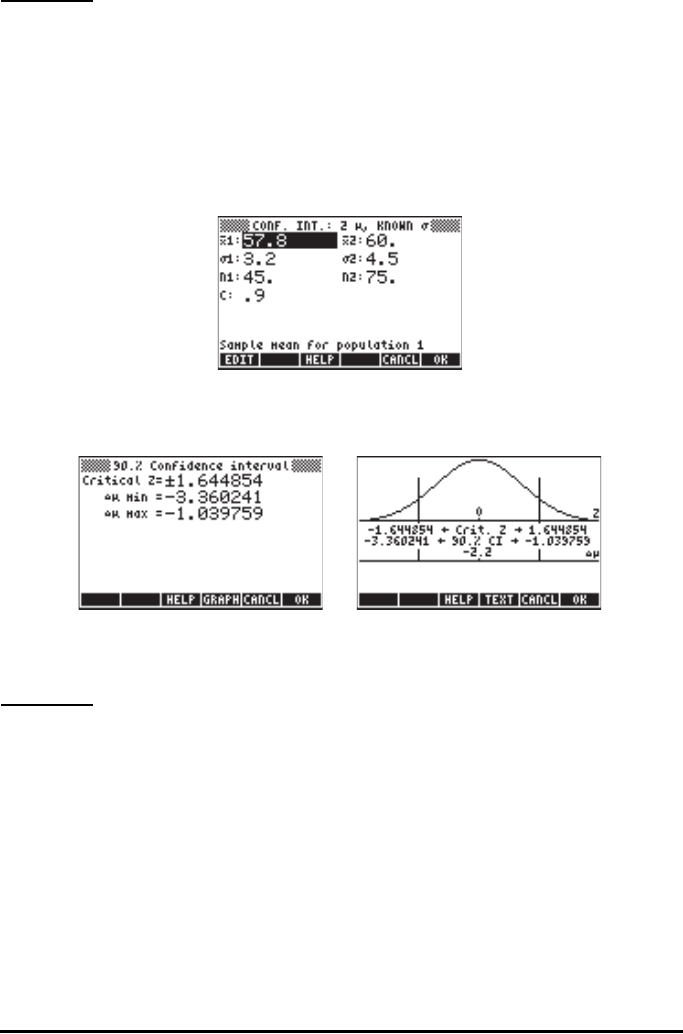
Example 2 -- Data from two samples (samples 1 and 2) indicate that ⎯x
1
=
57.8 and ⎯x
2
= 60.0. The sample sizes are n
1
= 45 and n
2
= 75. If it is
known that the populations’ standard deviations are σ
1
= 3.2, and σ
2
= 4.5,
determine the 90% confidence interval for the difference of the population
means, i.e., μ
1
- μ
2
.
Press ‚Ù—@@@OK@@@to access the confidence interval feature in the
calculator. Press ˜@@@OK@@@ to select option 2. Z-INT: μ 1 – μ2.. Enter the
following values:
When done, press @@@OK@@@. The results, as text and graph, are shown below:
The variable Δμ represents μ 1 – μ2.
Example 3
– A survey of public opinion indicates that in a sample of 150
people 60 favor increasing property taxes to finance some public projects.
Determine the 99% confidence interval for the population proportion that would
favor increasing taxes.
Press ‚Ù—@@@OK@@@to access the confidence interval feature in the
calculator. Press ˜˜ @@@OK@@@ to select option 3. Z-INT: μ 1 – μ2.. Enter the
following values: