Page 11-4
Matrix multiplication
Matrix multiplication is defined by C
m×n
= A
m×p
⋅B
p×n
, where A = [a
ij
]
m×p
, B =
[b
ij
]
p×n
, and C = [c
ij
]
m×n
. Notice that matrix multiplication is only possible if the
number of columns in the first operand is equal to the number of rows of the
second operand. The general term in the product, c
ij
, is defined as
This is the same as saying that the element in the i-th row and j-th column of the
product, C, results from multiplying term-by-term the i-th row of A with the j-th
column of B, and adding the products together. Matrix multiplication is not
commutative, i.e., in general, A⋅B ≠ B⋅A. Furthermore, one of the
multiplications may not even exist.
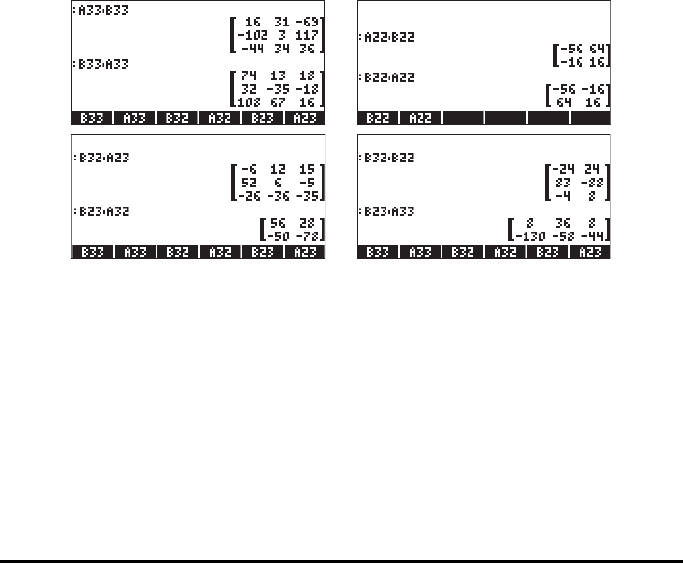
The following screen shots show the results of multiplications of the matrices that
we stored earlier:
!!!
The matrix-vector multiplication introduced in the previous section can be
thought of as the product of a matrix m×n with a matrix n×1 (i.e., a column
vector) resulting in an m×1 matrix (i.e., another vector). To verify this assertion
check the examples presented in the previous section. Thus, the vectors defined
in Chapter 9 are basically column vectors for the purpose of matrix
multiplication.
The product of a vector with a matrix is possible if the vector is a row vector,
i.e., a 1×m matrix, which multiplied with a matrix m×n produces a 1xn matrix
.,,2,1;,,2,1,
1
njmiforbac
p
k
kjikij
KK ==⋅=
∑
=


















