Filter
Top Products
Page 11-17
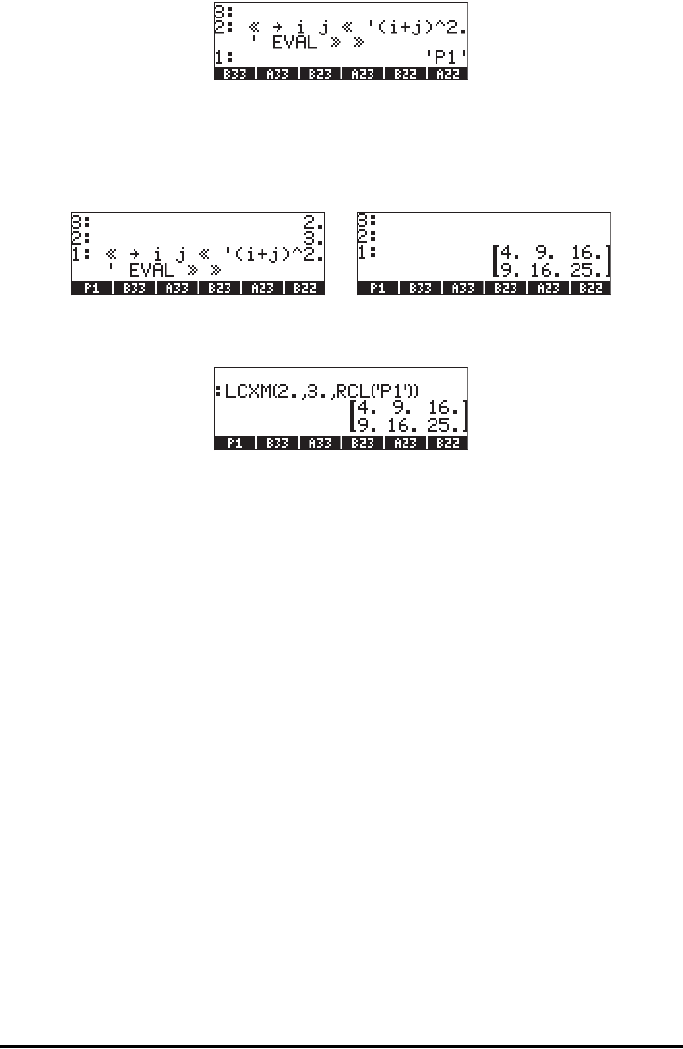
The implementation of function LCXM for this case requires you to enter:
2`3`‚@@P1@@ LCXM `
The following figure shows the RPN stack before and after applying function
LCXM:
In ALG mode, this example can be obtained by using:
The program P1 must still have been created and stored in RPN mode.
Solution of linear systems
A system of n linear equations in m variables can be written as
a
11
⋅x
1
+ a
12
⋅x
2
+ a
13
⋅x
3
+ …+ a
1,m-1
⋅x
m-1
+ a
1,m
⋅x
m
= b
1
,
a
21
⋅x
1
+ a
22
⋅x
2
+ a
23
⋅x
3
+ …+ a
2,m-1
⋅x
m-1
+ a
2,m
⋅x
m
= b
2
,
a
31
⋅x
1
+ a
32
⋅x
2
+ a
33
⋅x
3
+ …+ a
3,m-1
⋅x
m-1
+ a
3,m
⋅x
m
= b
3
,
. . . … . . !! .
. . . … . . !! .
a
n-1,1
⋅x
1
+ a
n-1,2
⋅x
2
+ a
n-1,3
⋅x
3
+ …+ a
n-1,m-1
⋅x
m-1
+ a
n-1,m
⋅x
m
= b
n-1
,
a
n1
⋅x
1
+ a
n2
⋅x
2
+ a
n3
⋅x
3
+ …+ a
n,m-1
⋅x
m-1
+ a
n,m
⋅x
m
= b
n
.
This system of linear equations can be written as a matrix equation, A
n×m
⋅x
m×1
= b
n×1
, if we define the following matrix and vectors: