Filter
Top Products
Page 16-44
and
The continuous spectrum is given by
The functions C(ω), S(ω), and A(ω) are continuous functions of a variable ω,
which becomes the transform variable for the Fourier transforms defined below.
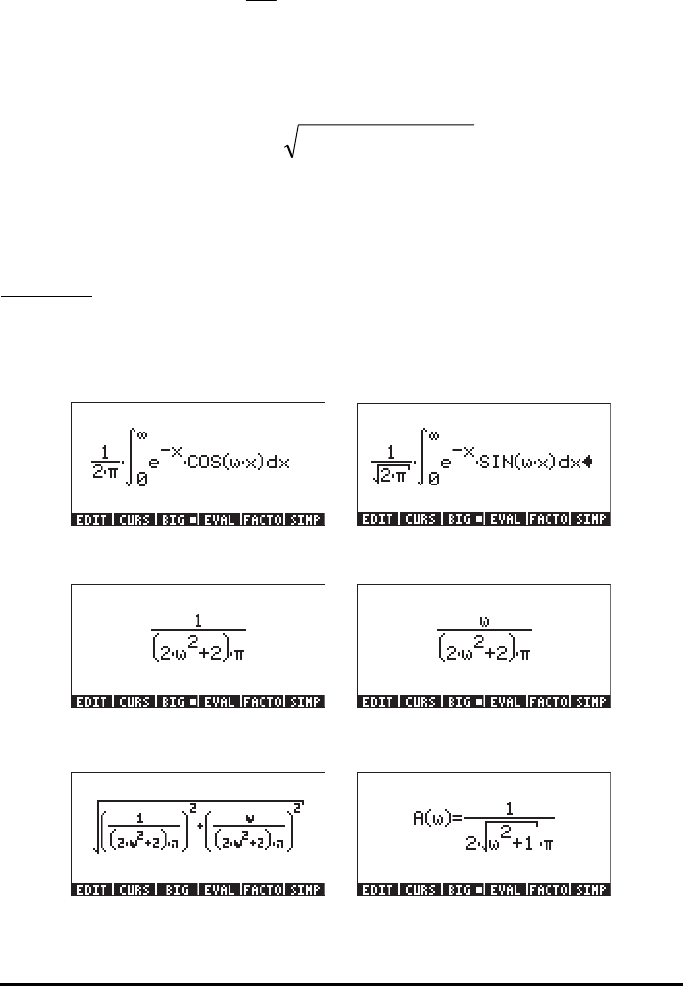
Example 1
– Determine the coefficients C(ω), S(ω), and the continuous spectrum
A(ω), for the function f(x) = exp(-x), for x > 0, and f(x) = 0, x < 0.
In the calculator, set up and evaluate the following integrals to calculate C(ω)
and S(ω), respectively. CAS modes are set to Exact and Real.
Their results are, respectively:
The continuous spectrum, A(ω) is calculated as:
.)sin()(
2
1
)(
∫
∞
−∞
⋅⋅⋅⋅= dxxxfS
ω
π
ω
22
)]([)]([)(
ωωω
SCA +=