Filter
Top Products
Page 16-26
f(t) = U
o
⋅[1-(t-a)/(b-1)]⋅[H(t-a)-H(t-b)].
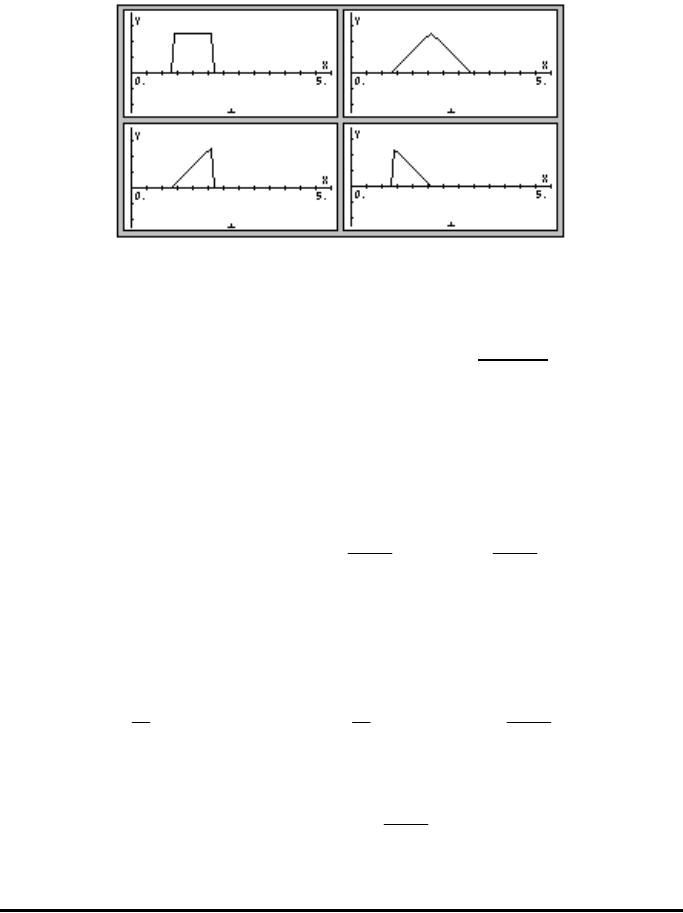
Examples of the plots generated by these functions, for Uo = 1, a = 2, b = 3, c
= 4, horizontal range = (0,5), and vertical range = (-1, 1.5), are shown in the
figures below:
Fourier series
Fourier series are series involving sine and cosine functions typically used to
expand periodic functions. A function f(x) is said to be periodic
, of period T, if
f(x+T) = f(t). For example, because sin(x+2π) = sin x, and cos(x+2π) = cos x,
the functions sin and cos are 2π-periodic functions. If two functions f(x) and g(x)
are periodic of period T, then their linear combination h(x) = a⋅f(x) + b⋅g(x), is
also periodic of period T. A T-periodic function f(t) can be expanded into a
series of sine and cosine functions known as a Fourier series given by
where the coefficients a
n
and b
n
are given by
∑
∞
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅+⋅+=
1
0
2
sin
2
cos)(
n
nn
t
T
n
bt
T
n
aatf
ππ
∫∫
−−
⋅⋅=⋅=
2/
2/
2/
2/
0
,
2
cos)(
2
,)(
1
T
T
T
T
n
dtt
T
n
tf
T
adttf
T
a
π
∫
−
⋅⋅=
2/
2/
.
2
sin)(
T
T
n
dtt
T
n
tfb
π