Page 16-11
Laplace transform and inverses in the calculator
The calculator provides the functions LAP and ILAP to calculate the Laplace
transform and the inverse Laplace transform, respectively, of a function f(VX),
where VX is the CAS default independent variable, which you should set to ‘X’.
Thus, the calculator returns the transform or inverse transform as a function of X.
The functions LAP and ILAP are available under the CALC/DIFF menu. The
examples are worked out in the RPN mode, but translating them to ALG mode is
straightforward. For these examples, set the CAS mode to Real and Exact.
Example 1
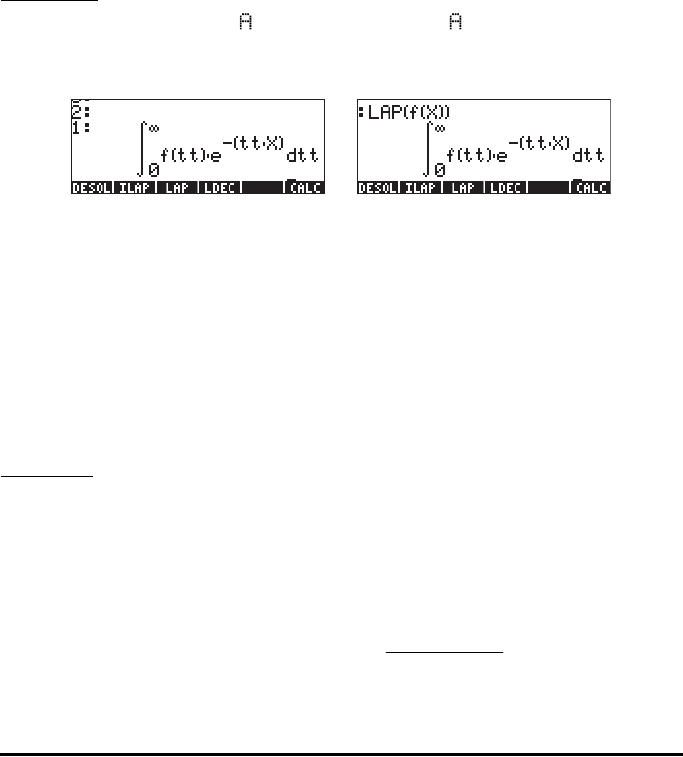
– You can get the definition of the Laplace transform use the
following: ‘f(X)’ ` LP in RPN mode, or L P(f(X))in ALG mode.
The calculator returns the result (RPN, left; ALG, right):
Compare these expressions with the one given earlier in the definition of the
Laplace transform, i.e.,
and you will notice that the CAS default variable X in the equation writer screen
replaces the variable s in this definition. Therefore, when using the function
LAP you get back a function of X, which is the Laplace transform of f(X).
Example 2
– Determine the Laplace transform of f(t) = e
2t
⋅sin(t). Use:
‘EXP(2*X)*SIN(X)’ ` LAP The calculator returns the result: 1/(SQ(X-2)+1).
Press μ to obtain, 1/(X
2
-4X+5).
When you translate this result in paper you would write
∫
∞
−
⋅==
0
,)()()}({ dtetfsFtf
st
L
54
1
}sin{)(
2
2
+⋅−
=⋅=
ss
tesF
t
L


















