Page 9-17
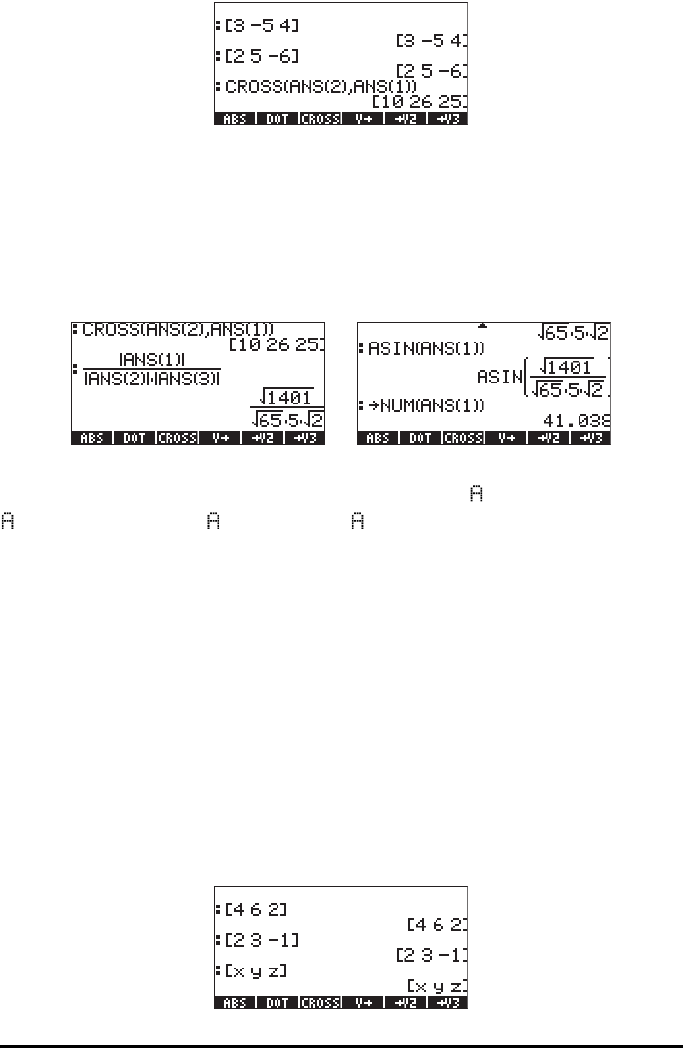
Thus, M = (10i+26j+25k) m⋅N. We know that the magnitude of M is such that
|M| = |r||F|sin(θ), where θ is the angle between r and F. We can find this
angle as, θ = sin
-1
(|M| /|r||F|) by the following operations:
1 – ABS(ANS(1))/(ABS(ANS(2))*ABS(ANS(3)) calculates sin(θ)
2 – ASIN(ANS(1)), followed by NUM(ANS(1)) calculates θ
These operations are shown, in ALG mode, in the following screens:
Thus the angle between vectors r and F is θ = 41.038
o
. RPN mode, we can
use: [3,-5,4] ` [2,5,-6] ` CROSS BS [3,-5,4] `
BS [2,5,-6] ` BS * / SIN NUM
Equation of a plane in space
Given a point in space P
0
(x
0
,y
0
,z
0
) and a vector N = N
x
i+N
y
j+N
z
k normal to
a plane containing point P
0
, the problem is to find the equation of the plane.
We can form a vector starting at point P
0
and ending at point P(x,y,z), a
generic point in the plane. Thus, this vector r = P
0
P = (x-x
0
)i+ (y-y
0
)j + (z-z
0
)k,
is perpendicular to the normal vector N, since r is contained entirely in the
plane. We learned that for two normal vectors N and r, N•r =0. Thus, we can
use this result to determine the equation of the plane.
To illustrate the use of this approach, consider the point P
0
(2,3,-1) and the
normal vector N = 4i+6j+2k, we can enter vector N and point P
0
as two
vectors, as shown below. We also enter the vector [x,y,z] last:


















