Filter
Top Products
Page 16-8
Example 2 -- Solve the second-order ODE:
d
2
y/dx
2
+ x (dy/dx) = exp(x).
In the calculator use:
‘d1d1y(x)+x*d1y(x) = EXP(x)’ ` ‘y(x)’ ` DESOLVE
The result is an expression having two implicit integrations, namely,
For this particular equation, however, we realize that the left-hand side of the
equation represents d/dx(x dy/dx), thus, the ODE is now written:
d/dx(x dy/dx ) = exp x,
and
x dy/dx = exp x + C.
Next, we can write
dy/dx = (C + exp x)/x = C/x + e
x
/x.
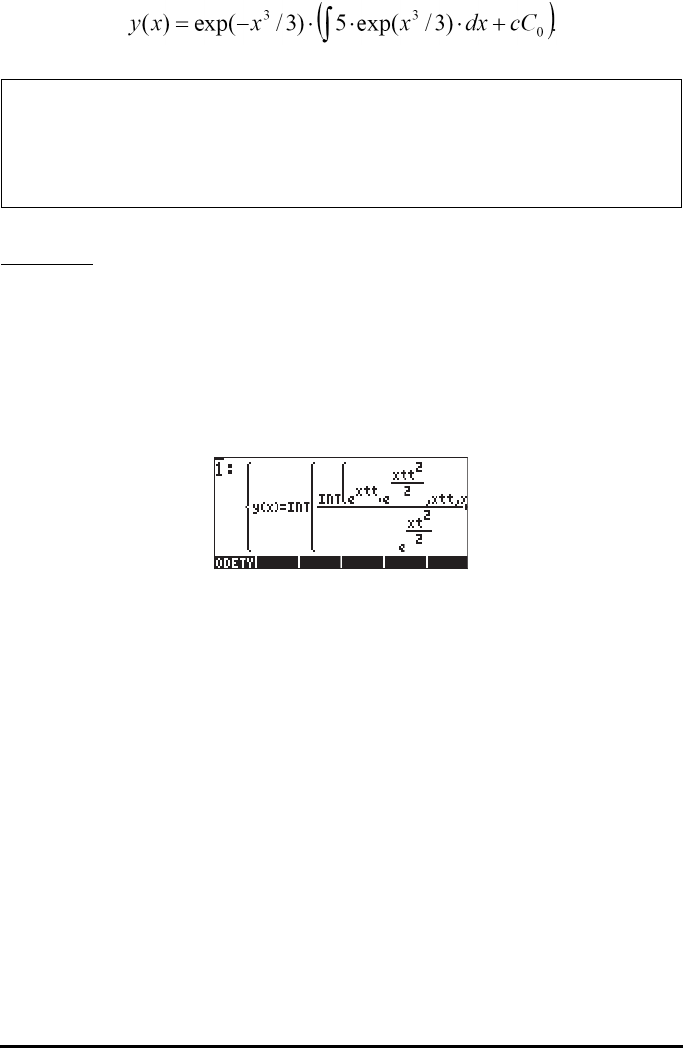
In the calculator, you may try to integrate:
‘d1y(x) = (C + EXP(x))/x’ ` ‘y(x)’ ` DESOLVE
The result is { ‘y(x) = INT((EXP(xt)+C)/xt,xt,x)+C0’ }, i.e.,
The variable ODETYPE
You will notice in the soft-menu key labels a new variable called @ODETY
(ODETYPE). This variable is produced with the call to the DESOL function and
holds a string showing the type of ODE used as input for DESOLVE. Press @ODETY
to obtain the string “
1st order linear”.