Filter
Top Products
Page 11-31
an expression = 0. Thus, the last set of equations is interpreted to be the
following equivalent set of equations:
X +2Y+3Z = 7,
Y+ Z = 3,
-7Z = -14.
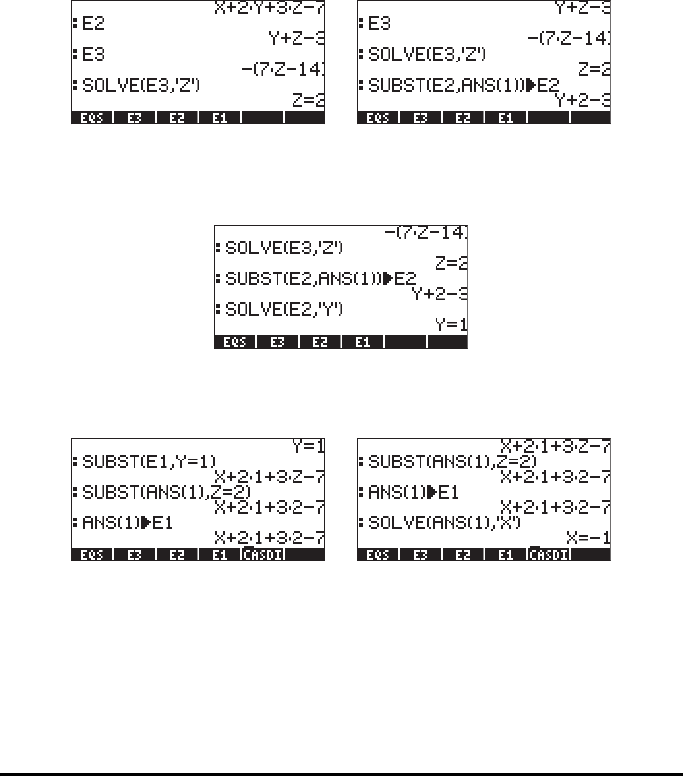
The process of backward substitution in Gaussian elimination consists in finding
the values of the unknowns, starting from the last equation and working
upwards. Thus, we solve for Z first:
Next, we substitute Z=2 into equation 2 (E2), and solve E2 for Y:
Next, we substitute Z=2 and Y = 1 into E1, and solve E1 for X:
The solution is, therefore, X = -1, Y = 1, Z = 2.
Example of Gaussian elimination using matrices
The system of equations used in the example above can be written as a matrix
equation A⋅x = b, if we use: