Filter
Top Products
Page 11-2
Addition and subtraction
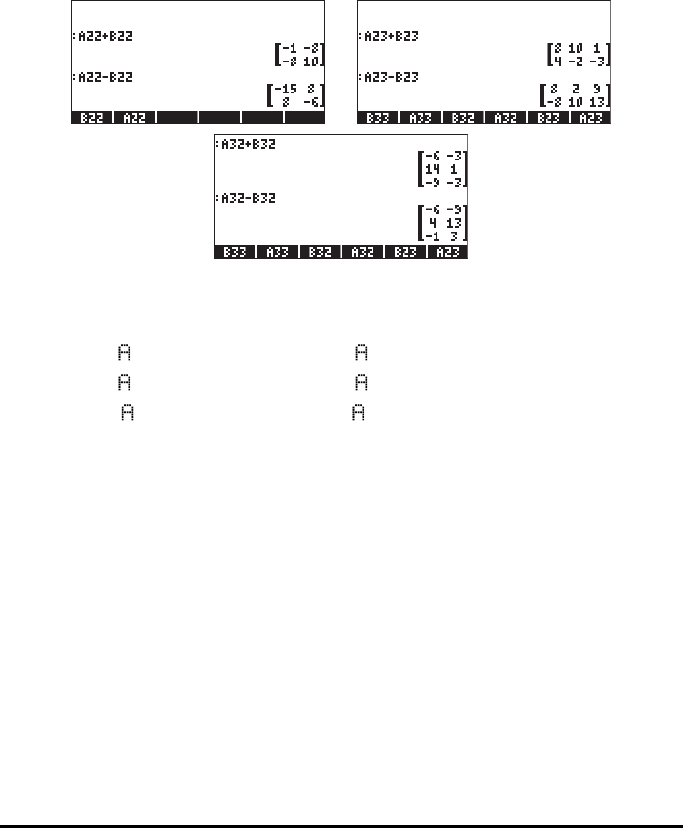
Consider a pair of matrices A = [a
ij
]
m×n
and B = [b
ij
]
m×n
. Addition and
subtraction of these two matrices is only possible if they have the same number
of rows and columns. The resulting matrix, C = A ± B = [c
ij
]
m×n
has elements c
ij
= a
ij
± b
ij
. Some examples in ALG mode are shown below using the matrices
stored above (e.g., @A22@ + @B22@)
In RPN mode, the steps to follow are:
22 ` B22`+ 22 ` B22`-
23 ` B23`+ 23 ` B23`-
32 ` B32`+ 32 ` B32`-
Translating the ALG examples to RPN is straightforward, as illustrated here. The
remaining examples of matrix operations will be performed in ALG mode only.
Multiplication
There are numerous multiplication operations that involve matrices. These are
described next.
Multiplication by a scalar
Multiplication of the matrix A = [a
ij
]
m×n
by a scalar k results in the matrix C =
kA = [c
ij
]
m×n
= [ka
ij
]
m×n
. In particular, the negative of a matrix is defined by
the operation -A =(-1)A = [-a
ij
]
m×n
. Some examples of multiplication of a
matrix by a scalar are shown below.