Page 18-26
Estimators for the mean and standard deviation of the difference and sum of the
statistics S
1
and S
2
are given by:
In these expressions, ⎯X
1
and ⎯X
2
are the values of the statistics S
1
and S
2
from
samples taken from the two populations, and σ
S1
2
and σ
S2
2
are the variances
of the populations of the statistics S
1
and S
2
from which the samples were
taken.
Confidence intervals for sums and differences of mean values
If the population variances σ
1
2
and σ
2
2
are known, the confidence intervals for
the difference and sum of the mean values of the populations, i.e., μ
1
±μ
2
, are
given by:
For large samples, i.e., n
1
> 30 and n
2
> 30, and unknown, but equal,
population variances σ
1
2
= σ
2
2
, the confidence intervals for the difference and
sum of the mean values of the populations, i.e., μ
1
±μ
2
, are given by:
If one of the samples is small, i.e., n
1
< 30 or n
2
< 30, and with unknown, but
equal, population variances σ
1
2
= σ
2
2
, we can obtain a “pooled” estimate of
the variance of μ
1
±μ
2
, as s
p
2
= [(n
1
-1)⋅s
1
2
+(n
2
-1)⋅s
2
2
]/( n
1
+n
2
-2).
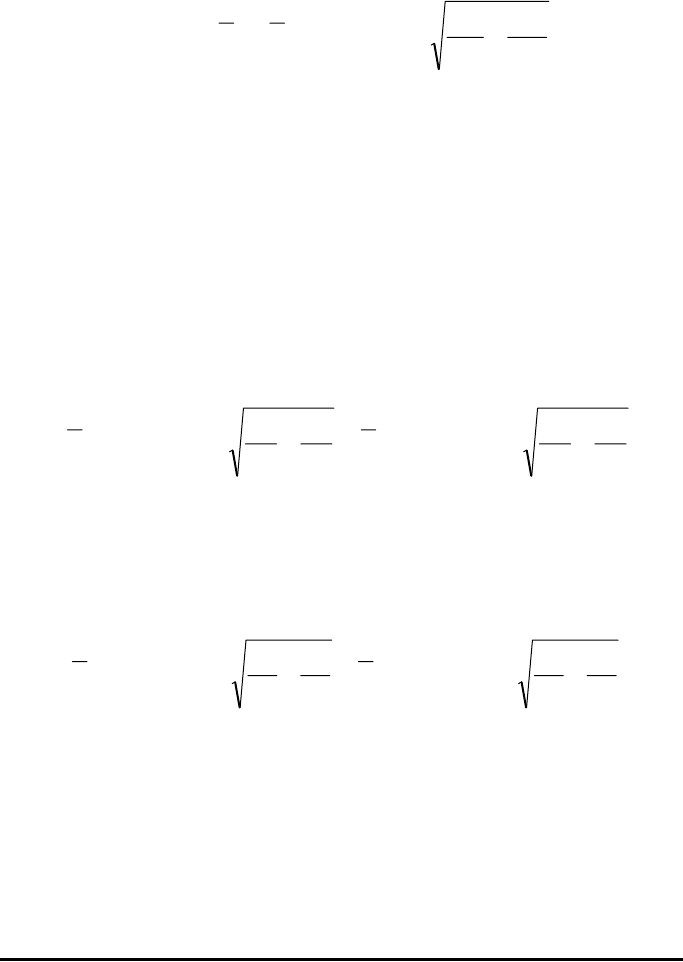
2
2
2
1
2
1
21
2121
ˆ
,
ˆ
nn
XX
SS
SSSS
σσ
σμ
+=±=
±±
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+⋅+±+⋅−±
2
2
2
1
2
1
2/21
2
2
2
1
2
1
2/21
)(,)(
nn
zXX
nn
zXX
σσσσ
αα
.)(,)(
2
2
2
1
2
1
2/21
2
2
2
1
2
1
2/21
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+⋅+±+⋅−±
n
S
n
S
zXX
n
S
n
S
zXX
αα


















