Filter
Top Products
Page 16-32
Or, in the calculator entry line as:
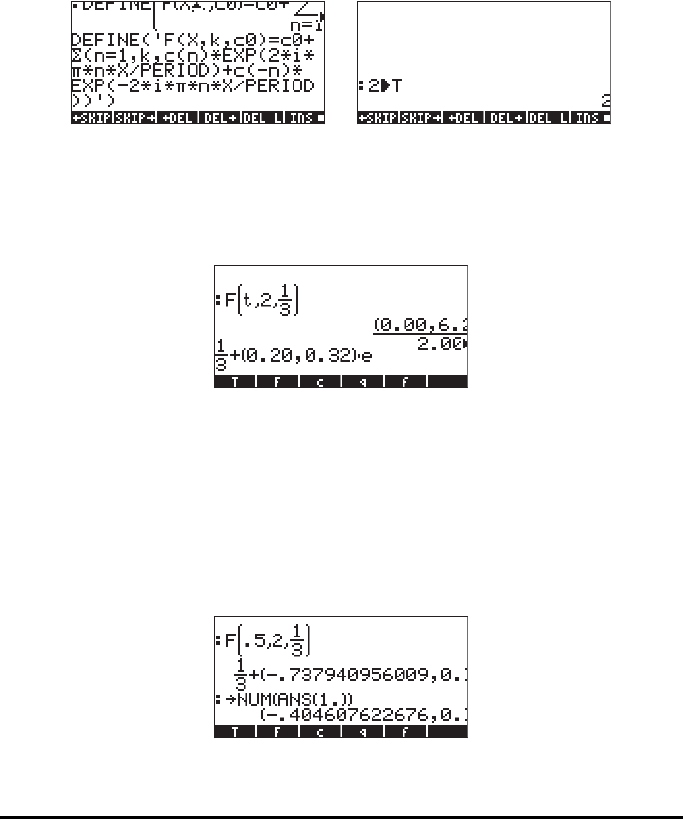
DEFINE(‘F(X,k,c0) = c0+Σ(n=1,k,c(n)*EXP(2*i*π*n*X/T)+
c(-n)*EXP(-(2*i*π*n*X/T))’),
where T is the period, T = 2. The following screen shots show the definition of
function F and the storing of T = 2:
The function @@@F@@@ can be used to generate the expression for the complex
Fourier series for a finite value of k. For example, for k = 2, c
0
= 1/3,and using
t as the independent variable, we can evaluate F(t,2,1/3) to get:
This result shows only the first term (c0) and part of the first exponential term in
the series. The decimal display format was changed to Fix with 2 decimals to
be able to show some of the coefficients in the expansion and in the exponent.
As expected, the coefficients are complex numbers.
The function F, thus defined, is fine for obtaining values of the finite Fourier
series. For example, a single value of the series, e.g., F(0.5,2,1/3), can be
obtained by using (CAS modes set to Exact, step-by-step, and Complex):