Page 16-68
The value of the solution, y
final
, will be available in variable @@@y@@@. This function
is appropriate for programming since it leaves the differential equation
specifications and the tolerance in the stack ready for a new solution. Notice
that the solution uses the initial conditions x = 0 at y = 0. If, your actual initial
solutions are x = x
init
at y = y
init
, you can always add these values to the
solution provided by RKF, keeping in mind the following relationship:
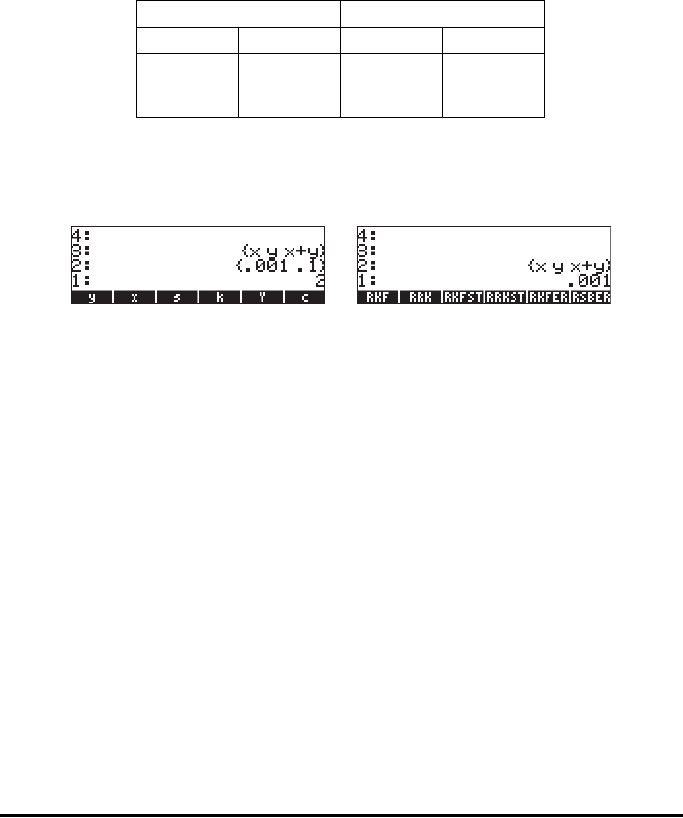
The following screens show the RPN stack before and after applying function
RKF for the differential equation dy/dx = x+y, ε = 0.001, Δx = 0.1.
After applying function RKF, variable @@@y@@@ contains the value 4.3880...
Function RRK
This function is similar to the RKF function, except that RRK (Rosenbrock and
Runge-Kutta methods) requires as the list in stack level 3 for input not only the
names of the independent and dependent variables and the function defining
the differential equation, but also the expressions for the first and second
derivatives of the expression. Thus, the input stack for this function will look as
follows:
ˆˍʳʳʳʳʳ {'x', 'y', 'f(x,y)' '∂f/∂x' '∂f/∂y' }
2: { εΔx }
1: x
final
The value in the first stack level is the value of the independent variable where
you want to find your solution, i.e., you want to find, y
final
= f
s
(x
final
), where f
s
(x)
represents the solution to the differential equation. The second stack level may
RKF solution Actual solution
xyxy
00
x
init
y
init
x
final
y
final
x
init
+ x
final
y
init
+ y
final


















