Filter
Top Products
Page 16-25
Example 4 – Plot the solution to Example 3 using the same values of y
o
and y
1
used in the plot of Example 1, above. We now plot the function
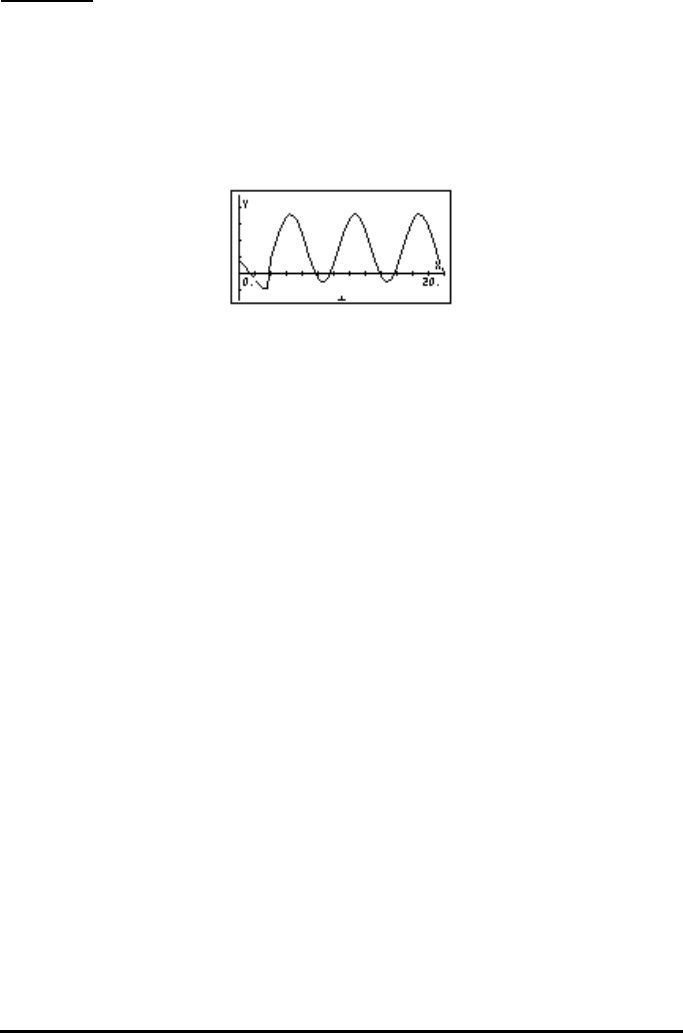
y(t) = 0.5 cos t –0.25 sin t + (1+sin(t-3))⋅H(t-3).
In the range 0 < t < 20, and changing the vertical range to (-1,3), the graph
should look like this:
Again, there is a new component to the motion switched at t=3, namely, the
particular solution y
p
(t) = [1+sin(t-3)]⋅H(t-3), which changes the nature of the
solution for t>3.
The Heaviside step function can be combined with a constant function and with
linear functions to generate square, triangular, and saw tooth finite pulses, as
follows:
Θ Square pulse of size U
o
in the interval a < t < b:
f(t) = Uo[H(t-a)-H(t-b)].
Θ Triangular pulse with a maximum value Uo, increasing from a < t < b,
decreasing from b < t < c:
f(t) = U
o
⋅ ((t-a)/(b-a)⋅[H(t-a)-H(t-b)]+(1-(t-b)/(b-c))[H(t-b)-H(t-c)]).
Θ Saw tooth pulse increasing to a maximum value Uo for a < t < b, dropping
suddenly down to zero at t = b:
f(t) = U
o
⋅ (t-a)/(b-a)⋅[H(t-a)-H(t-b)].
Θ Saw tooth pulse increasing suddenly to a maximum of Uo at t = a, then
decreasing linearly to zero for a < t < b: