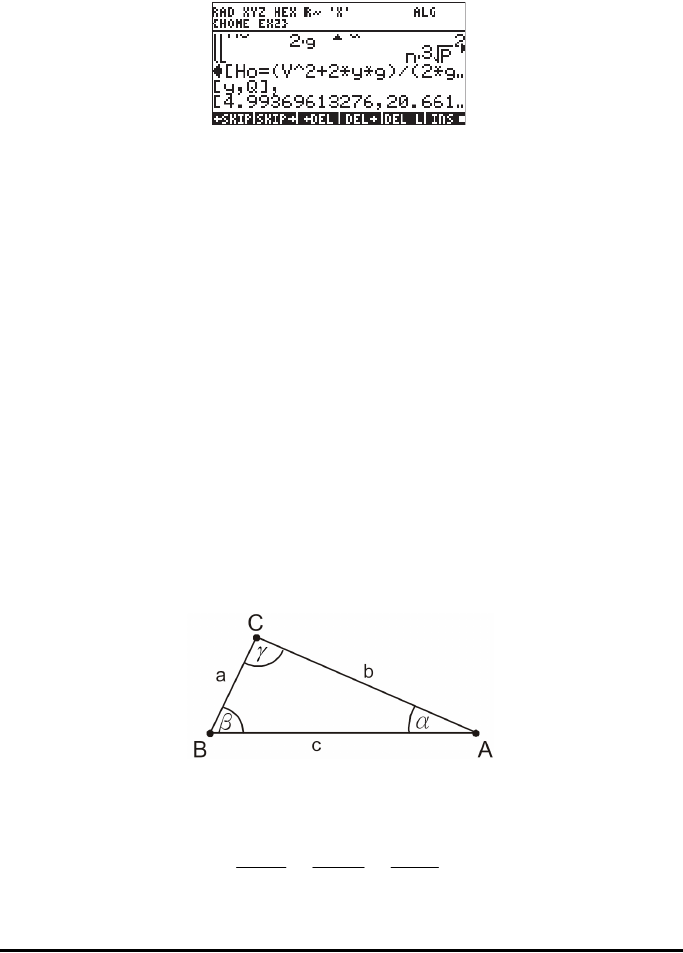
Page 7-9
The result is a list of three vectors. The first vector in the list will be the equations
solved. The second vector is the list of unknowns. The third vector represents the
solution. To be able to see these vectors, press the down-arrow key ˜ to
activate the line editor. The solution will be shown as follows:
The solution suggested is [4.9936.., 20.661…]. This means, y = 4.99 ft, and
Q = 20.661… ft
3
/s. You can use the arrow keys (š™—˜) to see the
solution in detail.
Using the Multiple Equation Solver (MES)
The multiple equation solver is an environment where you can solve a system of
multiple equations by solving for one unknown from one equation at a time. It
is not really a solver to simultaneous solutions, rather, it is a one-by-one solver of
a number of related equations. To illustrate the use of the MES for solving
multiple equations we present an application related to trigonometry in the next
section. The examples shown here are developed in the RPN mode.
Application 1 - Solution of triangles
In this section we use one important application of trigonometric functions:
calculating the dimensions of a triangle. The solution is implemented in the
calculator using the Multiple Equation Solver, or MES.
Consider the triangle ABC shown in the figure below.
The sum of the interior angles of any triangle is always 180
o
, i.e., α + β + γ =
180
o
. The sine law indicates that:
.
sinsinsin
cba
γβα
==


















