Appendix C: Algorithms
C–20
TVS600 & TVS600A Command Reference
One possible solution for dealing with the infinitely long impulse function, h(t)
is to reduce it to a manageable length. The simplest technique is to use the
central points of the filter and throw away the remaining points. What this does
is apply a time domain rectangular window filter to the impulse response h(t).
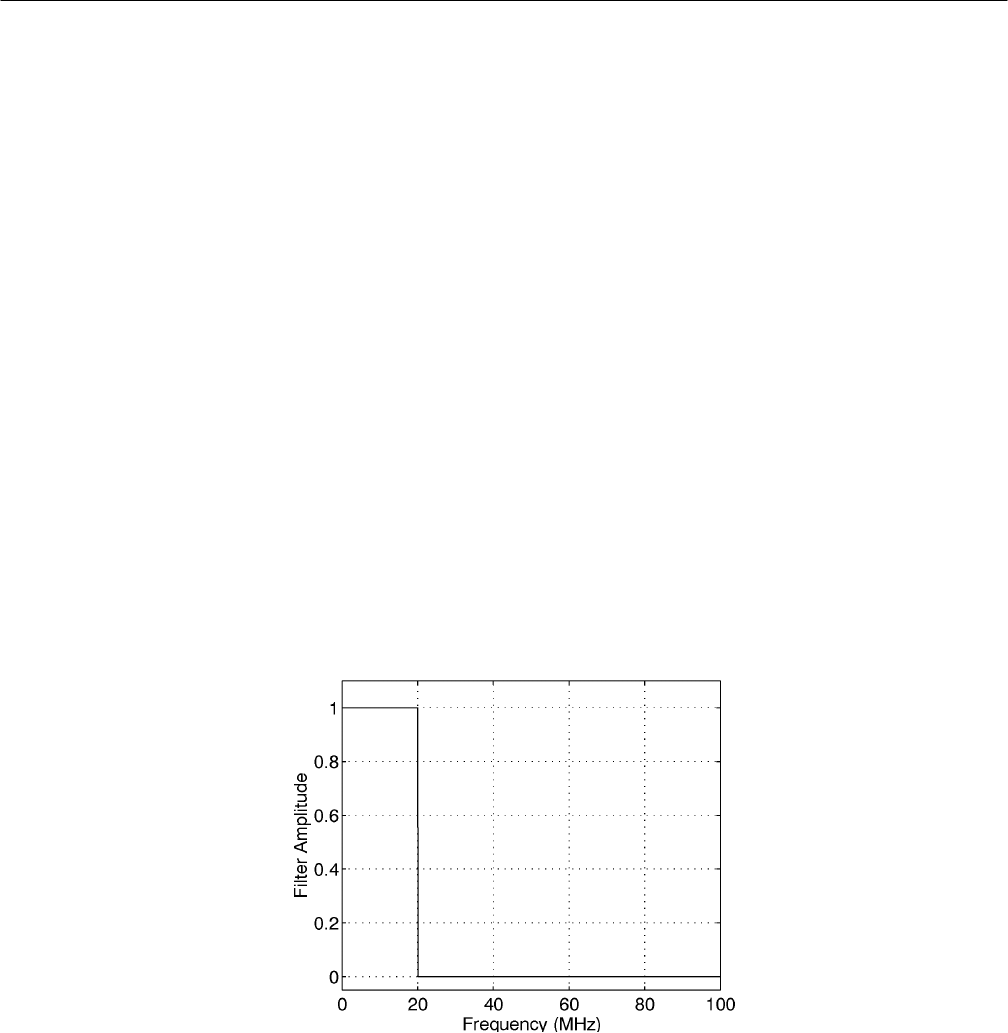
Figure C–5 shows the transfer function for an ideal lowpass filter. Figure C–6
shows the time domain impulse for the lowpass filter and depicts one possible
rectangular window which selects the central filter points.
Truncating the infinitely long impulse response of the filter to a finite length
results in a filter frequency response that is no longer ideal. In the time domain
the filter impulse response has been multiplied by a window w(t):
new h(t) + h(t) @ w(t)
To see how the frequency domain transfer function for the filter, H(f), has
changed it is necessary to transfer the above equation to the frequency domain.
Multiplication in the time domain corresponds to convolution in the frequency
domain.
W(f) + T
{
w(t)
}
New H(f) + H(f)*W(f)
Figure C–5: Transfer function for an ideal lowpass filter
Rectangular Window


















