Appendix C: Algorithms
C–28
TVS600 & TVS600A Command Reference
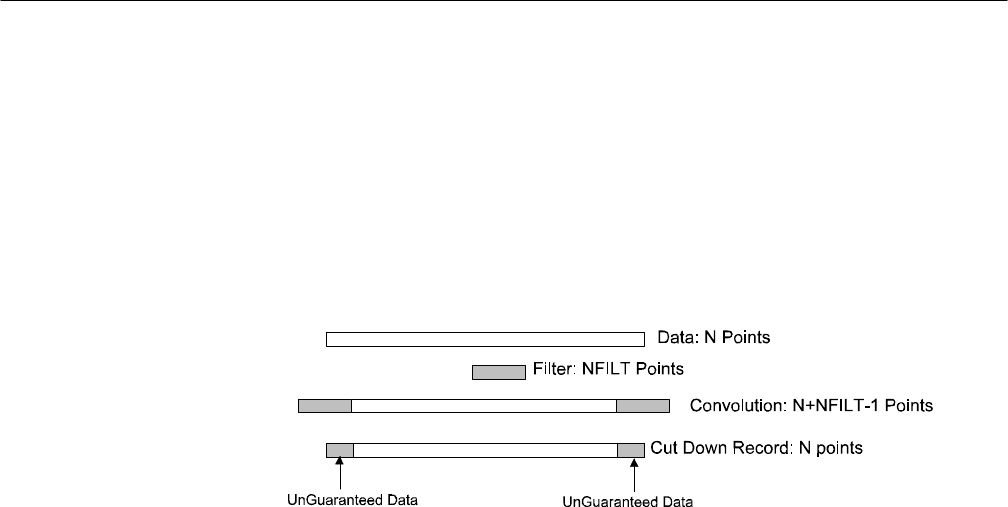
If the length of the original data is N and the length of the filter is NFILT, then
the result of the convolution is a record N+NFILT–1 points long. See Fig-
ure C–14. From this record, (NFILT–1)/2 points are cut off each end to return a
record which is N points long, the same size as the original record. However, the
filter specifications are not guaranteed throughout the length of the new data
record. For (NFILT–1)/2 points on either end of the new record, the data is
questionable. This is due to edge effects in the convolution when the filter record
is not fully within the data record.
Figure C–14: Record resulting from convolving the filter impulse response with the
waveform record
An example will help illustrate the edge effects. Figure C–15 shows a test signal
created from a 1 V amplitude, 10 MHz sine wave and a 0.5 V, 125 MHz sine
wave. This record is 500 points long, TINT=800 ps and the Nyquist frequency
F
nyq
=625 MHz. To filter out the high frequency signal, a lowpass filter was
applied with LPASS = 62.5 MHz, TWID=0.1 (TWIDHZ=62.5 MHZ) and
SREJ=26 dB. This resulted in a filter with b=1.51 and 53 points in the filter.
Figure C–16 shows the result of applying the lowpass filter to the data. The filter
did a good job of cutting out the high frequency components. To illustrate the
edge effects, Figure C–17 shows a close up view of the left end of the filtered
data and the 10 MHz sine signal. It is clear in that the filtered data does not
initially track the source 10 MHz sine signal.
On each end of the record, (NFILT–1)/2 data points of the filtered data are not
guaranteed to be within the specification of the filter. This is an undesirable
situation. To limit this effect, the waveform analyzer digital filter algorithm
limits the number of filter points to be a maximum of 10% of the acquisition
record length. With this constraint, in the worst case condition only 5% of the
data on either end of the filtered record is not guaranteed to be within the filter
specification. Hence, all measurements should be on the central 90% of the data
record.
To insure that your measurement does not include bad data, the waveform
analyzer sets the (NFILT–1)/2 data points on either end of the filtered record to
NULLs. The output waveforms of CALC blocks (which include the filter
function) are always floating point numbers. NULL points are defined as


















